오늘은 딥러닝을 위한 수학 2탄을 가지고 왔습니다!
딥러닝을 위한 수학 1탄에서는 벡터, 행렬의 미분을 다뤘고,
2023.01.24 - [Artificial Intelligence/혁펜하임 딥러닝 공부] - 딥러닝을 위한 수학 -1탄(스칼라, 벡터, 행렬, 미분)
딥러닝을 위한 수학 -1탄(스칼라, 벡터, 행렬, 미분)
딥러닝을 배울 때 필요한 수학에 빠질 수 없는 게 벡터, 행렬, 미분입니다. Back propagation이나 convolution 연산 등을 하기 위해 필수적입니다! 오늘은 스칼라와 벡터, 행렬, 이들의 미분에 대해서 공
univ-life-record.tistory.com
오늘은 확률 분포에 관해서 배워보겠습니다.
본 게시글은 패스트캠퍼스 [혁펜하임의 AI DEEP DIVE] 체험단 활동을 위해 작성되었습니다.
강의 퀄리티 너무 좋음 ㅎㅎ
1. 랜덤변수
랜덤 변수는 함수라고 생각하시면 됩니다.
예를 들어, 동전을 던질 때 나오는 경우는 앞, 뒤 두 가지 상황이 있습니다.
여기서 앞, 뒤를 숫자로(0,1) 표현해 주는 것을 랜덤변수로 만드는 과정이라고 생각해 주시면 돼요.
그러며 여기서 이 실수 값을 확률 값으로 바꿔주는 것이?
확률변수입니다.
앞면(1) → 1/2
뒷면(0) → 1/2
2. 확률 질량 함수, 확률 밀도 함수
확률 질량 함수 (PMF)는 딱딱 떨어지는 값을 가집니다.
예를 들면, 동전 던지기, 주사위 굴리기처럼 확률이 깔끔하게 나오는 경우.
확률의 합이 1이 되겠네요!
확률 밀도 함수(PDF)는 딱딱 떨어지지 않습니다.
특정 범위에서 확률을 구하고, 적분이 1이겠네요!
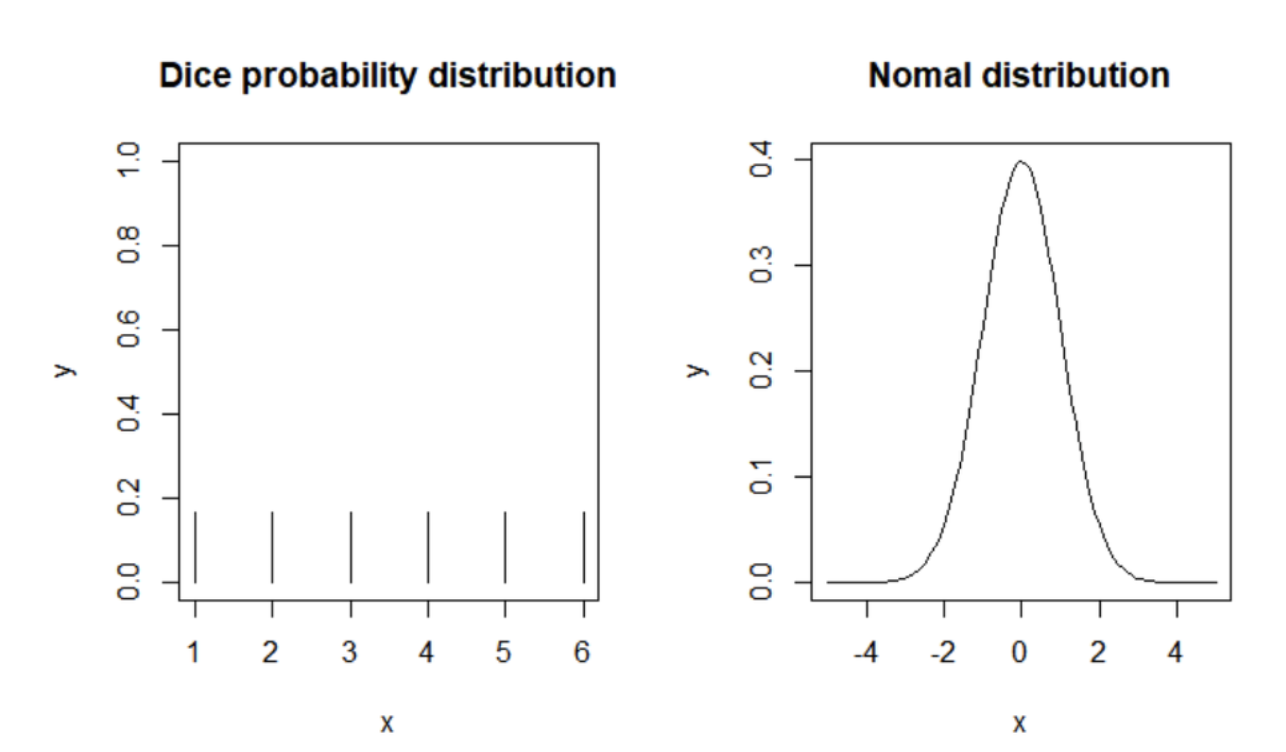
왼쪽(PMF), 오른쪽(PDF)
그림으로 보시면 훨씬 이해가 편하네요!
3. 평균과 분산
딥러닝에서 쓰는 평균은 기댓값입니다.
확률을 가진 사건을 무한히 반복했을 때 얻을 수 있는 값의 평균입니다.
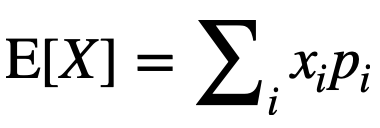
이렇게 랜덤변수와 그 확률 값을 곱해서 더해주면 됩니다.
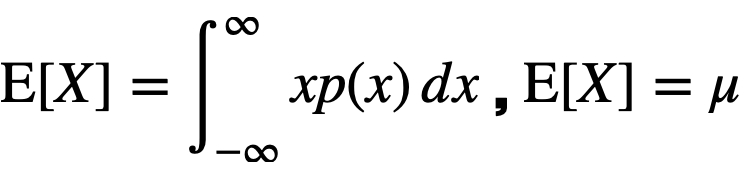
연속 랜덤 변수의 경우에는 적분을 해줍니다.
분산은 평균으로 설명하지 못하는 데이터의 분포를 설명해 줍니다.
데이터의 퍼진 정도를 나타내는 게 분산!
그래서 편차를 구합니다.
편차는 평균과의 차이!
편차 제곱의 평균을 구하면 분산이 됩니다.

참고로 표준편차는 단위를 맞추기 위해서 사용합니다!
4. 균등 분포와 정규 분포
균등 분포는 모든 사건들의 확률이 같습니다.

그래프를 보면 확률의 합은 1이어야 하기 때문에 f(x)의 값은 1/(b-a)가 됩니다.
평균 : (a+b)/2
분산 : (b-a)^2/12
정규 분포는 종모양 생각하시면 됩니다.

이 정도로 알고 계시면 됩니다.
5. MLE, MAP
간단하게 정리만 해볼게요!
최대 우도 추정(MLE)
이는 조건부확률과 비교하면 좋습니다.
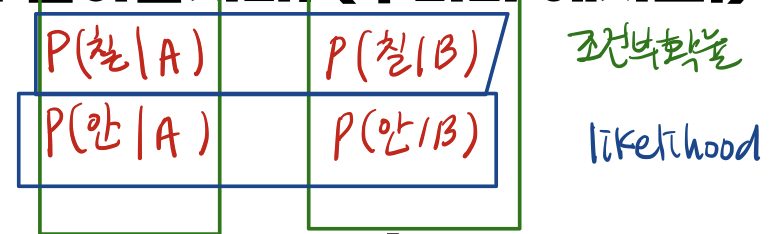
이렇게 우도(likelihood)는 뒤의 것의 함수로 보는 것입니다.
p(z|x)가 있을 때 measurement z를 보고 그 속에 숨어있는 x를 찾는 것!
x가 뭐였길래 measurement가 이렇게 나왔을까? 에 대한 답을 찾는 것이죠.
최대 사후 확률(MAP)
이는 우도(likelihood)뿐만 아니라 prior distribution까지 고려했다고 보면 됩니다.
내가 알고 싶은 x에 대한 사전 분포 정도는 알고 있다는 것이죠.
하지만 여기서 잘못된 사전 정보가 들어오면 오히려 추정 성능에 악영향을 줍니다.
MLE와 MAP를 잘 선택해서 쓰면 되겠죠? ㅎㅎ
제가 정리를 간략하게 하려고 노력했는데, 궁금한 점이 있으시면 답글 달아주세요! ^^
혁펜하임 DEEP DIVE 강의에서 혁펜하임 선생님의 높은 퀄리티 강의를 들으셔도 좋아요 ㅋㅋㅋㅋ
진짜 강추!!
'Artificial Intelligence > 혁펜하임 딥러닝 공부' 카테고리의 다른 글
| 인공지능 vs 머신러닝 vs 딥러닝 간단 설명 및 딥러닝 내부 알고리즘들(CNN, RNN, GAN) (6) | 2023.02.06 |
|---|---|
| 딥러닝을 위한 수학 -1탄(스칼라, 벡터, 행렬, 미분) (0) | 2023.01.24 |


댓글