딥러닝을 위한 수학 -1탄(스칼라, 벡터, 행렬, 미분)

딥러닝을 배울 때 필요한 수학에 빠질 수 없는 게 벡터, 행렬, 미분입니다.

Back propagation이나 convolution 연산 등을 하기 위해 필수적입니다!

 

오늘은 스칼라와 벡터, 행렬, 이들의 미분에 대해서 공부해 보겠습니다.

전치의 개념을 통해 더 쉽게! 미분할 수 있다는 점! 기대해 주세요 ㅎㅎ

(이 글은 혁펜하임의 AI DEE DIVE를 바탕으로 정리했습니다!)

 

---

1. 스칼라를 벡터로 미분

스칼라는 숫자 하나, 벡터는 숫자 여러 개! 

여기서는 그냥 편미분 해주시면 됩니다.

스칼라를 벡터로 미분

예를 들어

이 스칼라 함수를

이 벡터로 미분한다고 생각하면, 

[x2^2, 2*x1*x2]가 나올 것입니다.

하지만, 이 벡터가 매우 길다면.. 각각을 미분해 주기는 쉽지 않습니다.

 

그래서! 전치를 사용할 수 있습니다.

(뒤의 개념에서도 계속 쓰겠습니다!)

순간 변화량을 고려해서 df를 구해주고 

이를 전치를 사용한 벡터표현으로 바꿔줄 수 있습니다.

이렇게 df를 구해고 dx뒤에 곱해진 것이 우리가 구하고 싶은 미분 결과입니다!

 

2. 벡터를 벡터로 미분

 

여러 개의 입력이 들어가서 여러 개의 출력이 나오는 것!

이것도 각각을 미분해 줘도 되지만, 전치를 사용할 수 있습니다.

다음과 같이 나타낼 수 있겠네요!

여기서 f, x는 벡터를 나타냅니다.

따라서 위와 같이 dx 뒤에 있는 것들이 미분값(A)이 됩니다.

 

(추가)

벡터의 미분에서는 앞으로 앞으로의 연쇄법칙이 성립

 

3. 스칼라를 행렬로 미분

 

행렬식스칼라 값을 각각의 행렬 변수에 따라 미분해주면 되죠?

여기서도 전치를 사용해서 나타내겠습니다.

하지만 행렬은 tr(trace) 함수에 대해 알아야 합니다.

별거 없습니다!

그냥 대각선 값들을 더해주는 게(왼쪽 위에서 오른쪽 아래로) trace함수입니다 ㅋㅋㅋ...

 

자, 우리가 얻고 싶은 식은

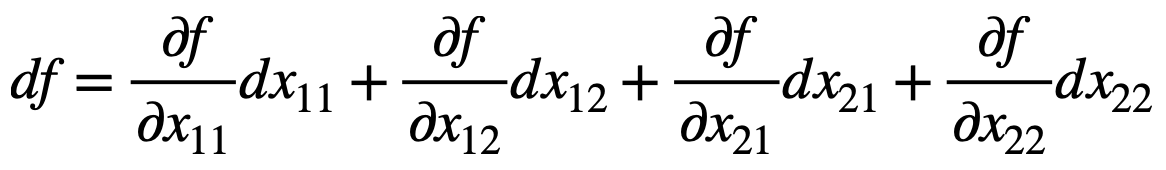
이 식입니다. 

이 식을

위의 두 식으로 나타내야 합니다. trace함수를 이용하면,

이렇게 나타낼 수 있습니다.

(각각 행렬의 곱을 통해서 결과 행렬의 1행 1열과 2행 2열 값이 우리가 얻고자 하는 값, 즉 tr함수에 넣은 값)

앞의 경우들과 tr이 붙은 것 말고는 달라지는 게 없습니다!

 

4. 행렬을 행렬로 미분

이는 딥러닝에서 자주 쓰이지는 않습니다.

하지만 알고 있으면 좋으니까 ㅎㅎ

간단하게만 정리해 보자면,

행렬의 경우에는 행렬을 벡터로 바꾼 다음 벡터를 벡터로 미분하는 방식을 적용합니다.

즉, 모든 부분이 다 똑같고

이렇게 vec가 붙은 것만 달라졌습니다.

 

5. 벡터를 행렬로 미분

위와 같이 x벡터와 w행렬이 있다면,

w행렬을 벡터로 나타내자.

그리고 y, x, w의 관계식을 적어주면

이렇게 쓸 수 있다.

그리고 y를 w에 대해 미분해 주기 위해 전치를 사용하면,

여기서 I2는 항등행렬이다. 

다음시간에는 확률분포에 관해 정리해보겠습니다.