안녕하세요!
오늘은 반도체 단위 공정 중 하나인 diffusion에 대해 배워보겠습니다.
Diffusion의 fick's law를 들어가기 전에 두 가지를 먼저 보고 가겠습니다.
1. Flux
diffusion을 배우려면 가장 기본적으로 알아야 하는게 Flux입니다.
Flux가 뭘까요?
Flux = (#, mol수, 원자의 개수) / (단위시간 * 단위면적)
단위시간 동안 단위면적에 지나가는 원자의 개수라고 쉽게 생각하시면 됩니다!!
2. Diffusion coefficient(D)

Diffusion coefficient(D)는 다음 식과 같이 쓰입니다.
Diffusion이라는 것 자체가 특정 물질 A가 특정 물질 B로 확산되는 것을 의미합니다.
즉, 특정 물질 A가 특정 물질 B로 확산될 때 정해지는 진짜 상수 D0와 EA가 존재합니다.
(예를 들어 Boron이 FCC구조의 Si로 diffusion 된다면 그때의 D0와 EA가 정해져 있습니다.)
그러면 D를 결정하는 요소는 T(온도)가 됩니다.
온도가 올라갈수록 Diffusion이 잘됨을 의미합니다!
Diffusion coefficient의 단위는
m^2/s입니다.
이제 Fick's Law에 대해서 배워보겠습니다!
Fick's law는 확산 flux에 관한 법칙입니다.
제1법칙과 2법칙이 있는데, 차례대로 봐보겠습니다!
1. Fick's first Law
Steady-state diffusion
Steady-state는 시간에 따른 변화가 없는 것을 의미합니다.
즉, Jin과 Jout이 같은 것이죠!
들어가는 flux와 나오는 flux가 같습니다.
그래서 여기서의 Flux에 관한 식을 쓰면

이렇습니다. 왜냐구요?
식의 단위를 보시면 됩니다.
위에서 구한 D와 C(농도/단위부피)를 곱해보면
(cm^2/s) * (개수/cm^4) = 개수/(cm^2 * s)
이렇게 돼서 Flux가 나오는 것을 확인하실 수 있습니다.
그리고 저 식은 diffusion이 시작된 곳과 끝점에서 같습니다.
steady-state이기 때문!!

그림으로 보면 저렇게 거리에 따른 농도의 기울기가 같습니다.
알아야 할게, Steady-state를 가정했기 때문에 시간에 대한 변수가 없고
x축 길이에 대한 변수만 존재합니다.
2. Fick's second law
두 번째 법칙은 non steady state입니다.
즉, 시간에 따라서 농도가 변화하고,
더 이상 Jin과 Jout이 같지 않습니다.
지금부터 식을 유도해 보겠습니다!
어렵지 않으니 차근차근해봅시다.


자, 맨 왼쪽 M은 질량입니다.
가운데 식은 농도차이에 (면적*길이)를 곱했습니다.
즉, 농도차 * 부피이고 이는 질량을 의미합니다.
맨 오른쪽 식은 flux에 (면적*시간)을 곱했습니다.
Flux = (무게 or 개수 / 면적 * 시간)
여기에 (면적 * 시간)을 곱해주게 되면 무게만 남게 됩니다.
따라서 위 식은 성립합니다.
이를 정리해 보면
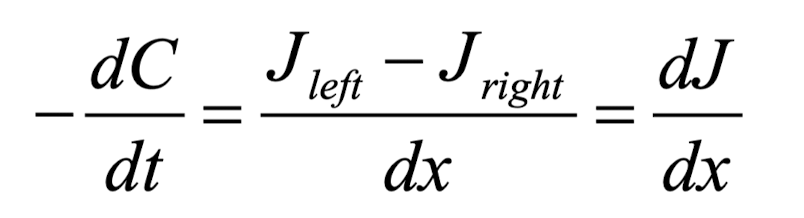
이렇게 나오고, J 자리에 제1법칙에서 구한 Flux값을 넣어주겠습니다.
그렇게 해주면
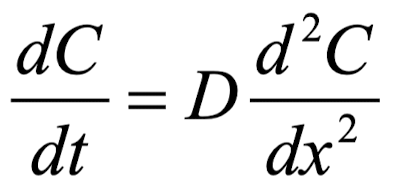
이렇게 나오고,
Non steady-state이기 때문에 시간에 대한 변수가 있는 것을 확인하실 수 있습니다.
보통의 상황은 non steady-state 상황입니다.
공정상황을 가정해 보면,
온도를 T로 설정하고, 어떤 물질을 diffusion 시킨다고 할 때 D값을 구할 수 있습니다.
그리고 저 식을 풀어주게 되면 시간과 거리에 따른 농도를 구할 수 있습니다.
반대로, 특정 시간 동안 특정 거리 x에서 농도를 결정했다면,
식을 통해 온도 T를 어떻게 설정해야 할지 구할 수 있습니다.
만일 rough하게 어느정도 시간이 지나야 diffusion될지 결정하려면 어떻게 하면 될까요?
Steady state 상태에서 해석하면 됩니다.
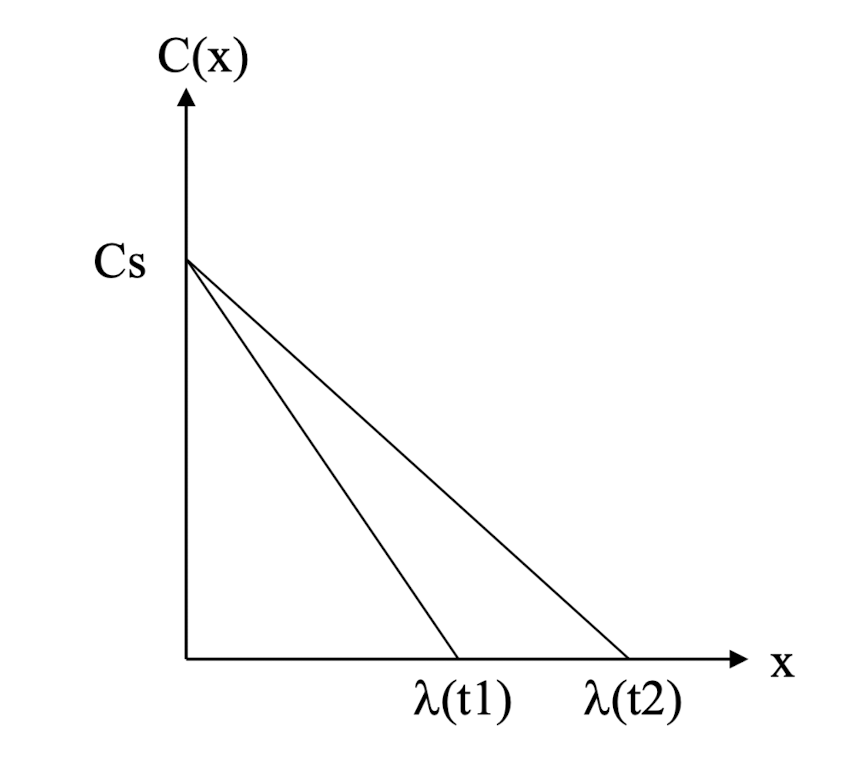
이 그래프를 보면 거리에 따른 농도의 기울기가 일정하기 때문에
steady state(시간에 따라 Flux의 변화가 없음)인 것을 확인할 수 있습니다.
그 그래프 아래의 넓이를 구하면 전체 농도가 나옵니다.
근데, 거리와 농도를 곱하기 때문에
농도(#개수/부피) X 거리 = #개수/면적
면적 당 개수(dose)가 나오게 됩니다.
그러면 이를 시간에 대해 나눠주면 Flux가 나옵니다.
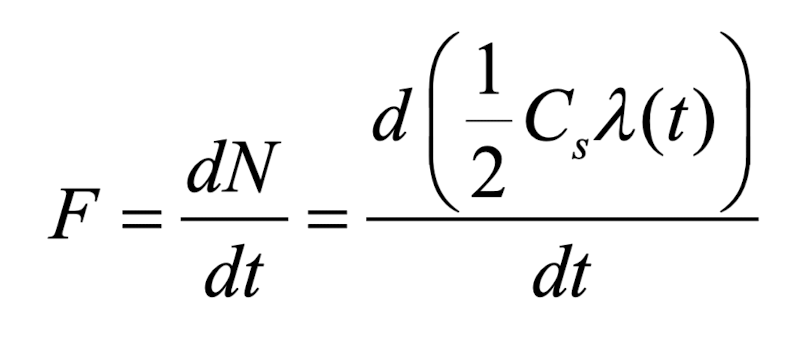
그러면 steady-state이기 때문에 위에서 구한 Flux와 같다고 해줍니다.
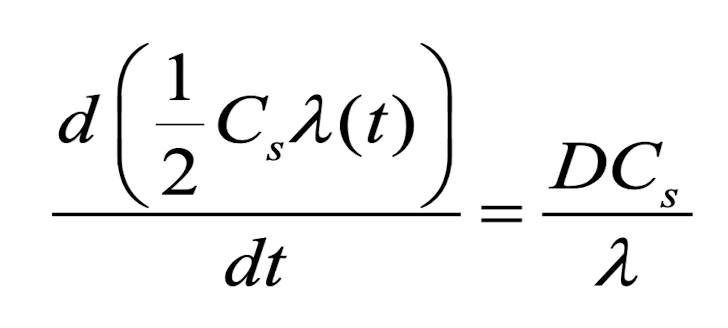
그럼 이렇게 나오고
이를 정리해주면
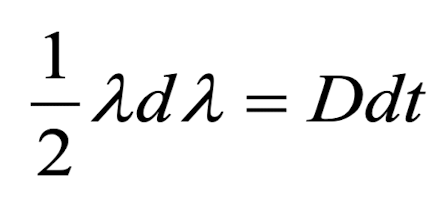
이런 결과를 얻습니다.
즉,
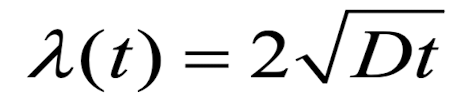
이렇게 나오기 때문에
시간을 길게 해줘도 Diffusion된 거리는 별로 변화하지 않습니다.
오늘은 여기까지!!
마지막 내용이 핵심입니다!ㅋㅋㅋ
공정상황에서 어떻게 사용할지 잘 한번 생각해 보세요 ㅎㅎ
오늘도 수고 많았습니다!
'반도체 연구하기 > Semiconductor processing(반도체 공정)' 카테고리의 다른 글
| Ion Implantation(이온주입공정) : 수식으로 이해하기, 모델링하기, 가우시안 분포 (0) | 2024.08.12 |
|---|---|
| 반도체 공정 : Ion implantation(이온주입공정)_1탄. Diffusion(확산공정)과의 비교, 중요 파라미터들 (0) | 2024.04.06 |
| Thermal Oxidation(산화 공정) 3분만에 깊게 이해하기! SiO2가 반도체 공정에서 쓰이는 곳! (0) | 2023.06.23 |
| Oxidation - Deal-Grove Model(산화, 딜 그루브 모델) 쉽게 이해하기! (0) | 2023.06.22 |
| Wafer Cleaning(RCA cleaning, post CMP cleaning) (0) | 2023.06.21 |




댓글