안녕하세요!
오늘은 이온주입공정을 공부할 겁니다.
우리가 이온을 주입할 때 에너지 강도에 따라, 원자에 따라 달리 깊이도 바뀌고 분산도 바뀐다고 배웠습니다.
이를 수식적으로 모델링하는 과정을 설명하겠습니다.
(본 포스팅은 서울과학기술대학교 김사라은경 교수님의 ppt자료를 참고했습니다.)
1. Gaussian Distribution(가우시안 분포)
(Normal distribusion)
원래는 더 복잡한 형태로 이온주입공정이 이루어지지만
우리는 수식적으로 모델링해보는 것이 목적이기 때문에 간단히 가우시안 분포를 사용할 것입니다.

식은 이와 같습니다.
μ : 평균
σ : 표준편차
이를 이온주입공정 식으로 모델링할 것입니다.
2. Ion implantation modeling
x는 원자가 들어가는 거리,
μ는 원자가 들어가는 평균 거리 → R_p
σ는 원자가 평균으로부터 얼마나 퍼지는지 → △R_p
exponential 앞의 상수는 Cmax로 치환

이를 그림으로 보면 다음과 같습니다.

3. The number of implanted ions(Q)
이번에는 Implanted ion의 양과 위 수식의 연관성을 보겠습니다.
C(x)는 결국 x위치에서의 implanted ions의 농도입니다.
따라서 이를 전체구간에서 적분해주면
총이온의 양이 나오게 됩니다.

위와 같은 식으로 정리할 수 있고,
아래의 가우시안 함수의 적분공식을 이용하면

전체 Implanted ion의 개수는

이렇게 표현가능합니다.
보통 Q(주입한 이온의 양)는 공정할 때 우리가 넣어주는 known값입니다.
따라서 △R_p를 알아내서 Cmax를 유추할 수 있다는 것이 핵심입니다.!!
(여기서 △R_p는 뒤에서 어떻게 구하는지 보겠습니다 :))
4. FWHM(Full-Width Half-Maximum) △X_p
이는 위에서 구한 공정 수식에서 Cmax의 절반이 되는 지점의 x거리 폭을 의미합니다.
일단 어디에 쓰는지 알기 전에!
식으로 정리하면,

이를 의미하기 때문에 C(x)를 대입해 주면

다음과 같이 정리됩니다.
이를 구한 이유는
1. FWHM을 알 수 있는 상황이라면 △R_p를 구할 수 있고 이를 통해 Cmax를 구할 수 있습니다.
2. XRD measurement를 이용할 때
Scherrer's Equation을 사용하곤 합니다.

β : FWHM
τ : grain 크기, 결정 크기
이를 통해 FWHM(반치폭)을 구해서 grain크기나 crystalline 등에 대한 정보를 얻을 수 있습니다.
5. Relationships between R_p, △R_p, R
가우시안 분포의 특징을 이용해 수식을 구하면,


다음과 같은 두 개의 식을 얻을 수 있습니다.
이 식이 주어졌을 때 무엇을 알 수 있을까요?
1) M_t << M_p
R_p / R → 1
R_p : 직선거리
R : scattering 하며 가는 거리
즉, lateral scattering이 거의 없이 직진한다는 의미입니다.
2) M_p << M_t
R_p / R → very small
즉, lateral scattering이 매우 크게 발생한다는 의미입니다.
따라서 다음과 같이 그림으로 나타낼 수 있겠네요!
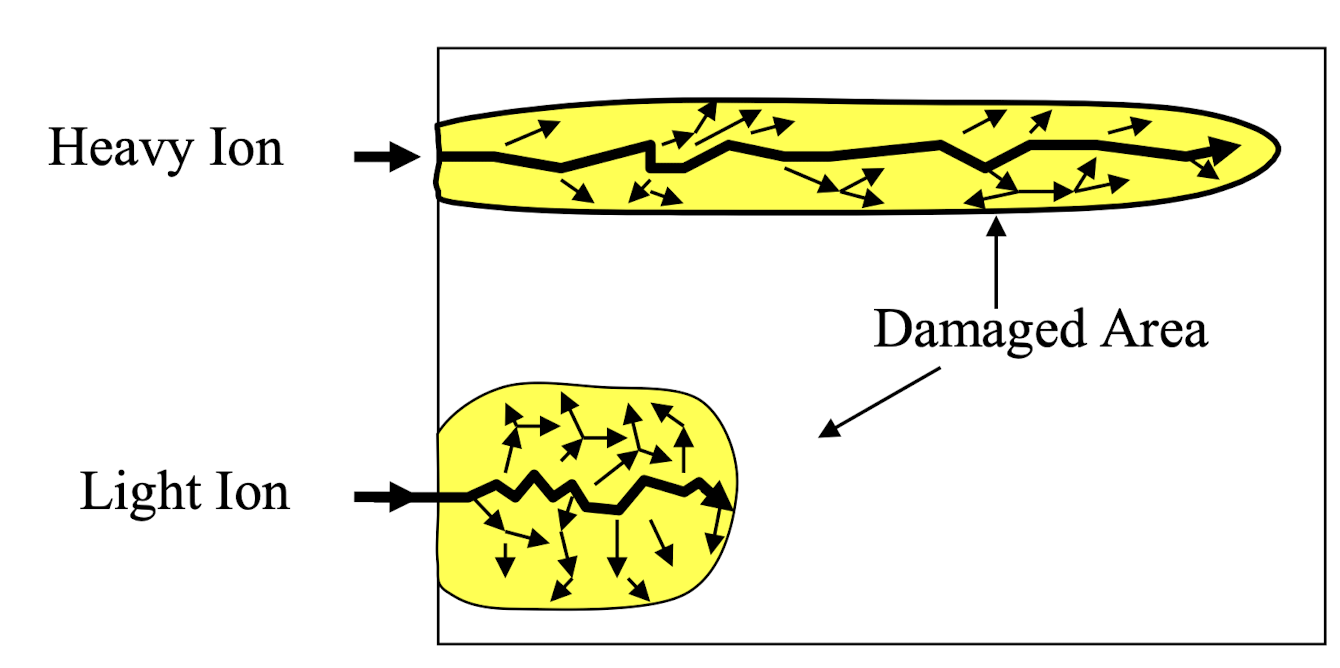
3) M_p = M_t
여기서는 △R_p에 대해 살펴볼 것입니다.
1,2의 경우에 이 값은 거의 0에 가깝습니다. (수식에 대입해 보면)
하지만 3번 상황에서는
△R_p / R_p → 1/3
이 상황에서 표준편차가 가장 큰 것을 알 수 있습니다.
이는 이온주입공정의 최대 퍼짐을 나타냅니다.
왜냐하면 △R_p 식을 봤을 때 산술기하 평균을 통해 M_t와 M_p가 값이 같을 때 최댓값을 가지니까요!
6. 실제 문제 해결
A process engineer building an NMOS device wants to dope the polysilicon at the same time as doing the arsenic source/drain diffusion. The source drain implant dose is 2 ×10^15cm−2 at an energy of 50 keV.
For the above implant conditions, what is the minimum polysilicon thickness that can be used if the implant is not to affect the channel doping which is 1 ×10^16cm−3 near the surface. (assume the gate oxide is negligibly thick compared to the polysilicon)
(아래 그림을 이용)
출처 : silicon-vlsi-technology
다음과 같은 상황이 있습니다.
문제 해석부터 어렵습니다! ㅋㅋㅋ
하지만 해답은 매우 간단하다는 것!
먼저 생각해 보시고!! 제가 풀어보겠습니다.
해답:
일단 Source/Drain을 2x10^15cm-2의 농도로 50 keV 에너지를 가지고 implant 한답니다.
이때 channel doping이 10^-16으로 되어있으니 이를 침범하지 않는 최소 polysilicon mask두께(xm)를 구하라는 문제입니다.
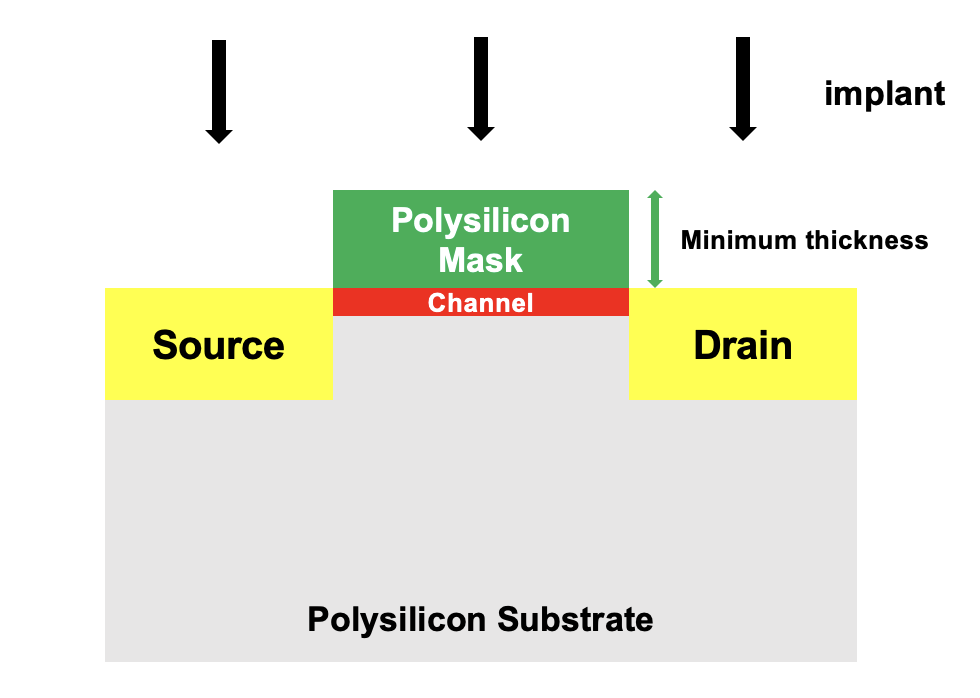
이를 그림으로 나타내봤습니다.
자, Polysilicon thickness를 구하기 위해 C(x)식을 사용해야 합니다.
C(x) = channel 농도(10^-16)가 되는 순간 멈춰야 하는 것입니다!
이때의 x를 구하면 그게 mask thickness(xm)가 되겠네요!

이 식을 가져왔습니다.
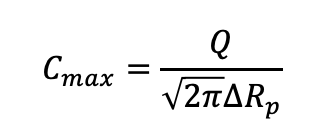
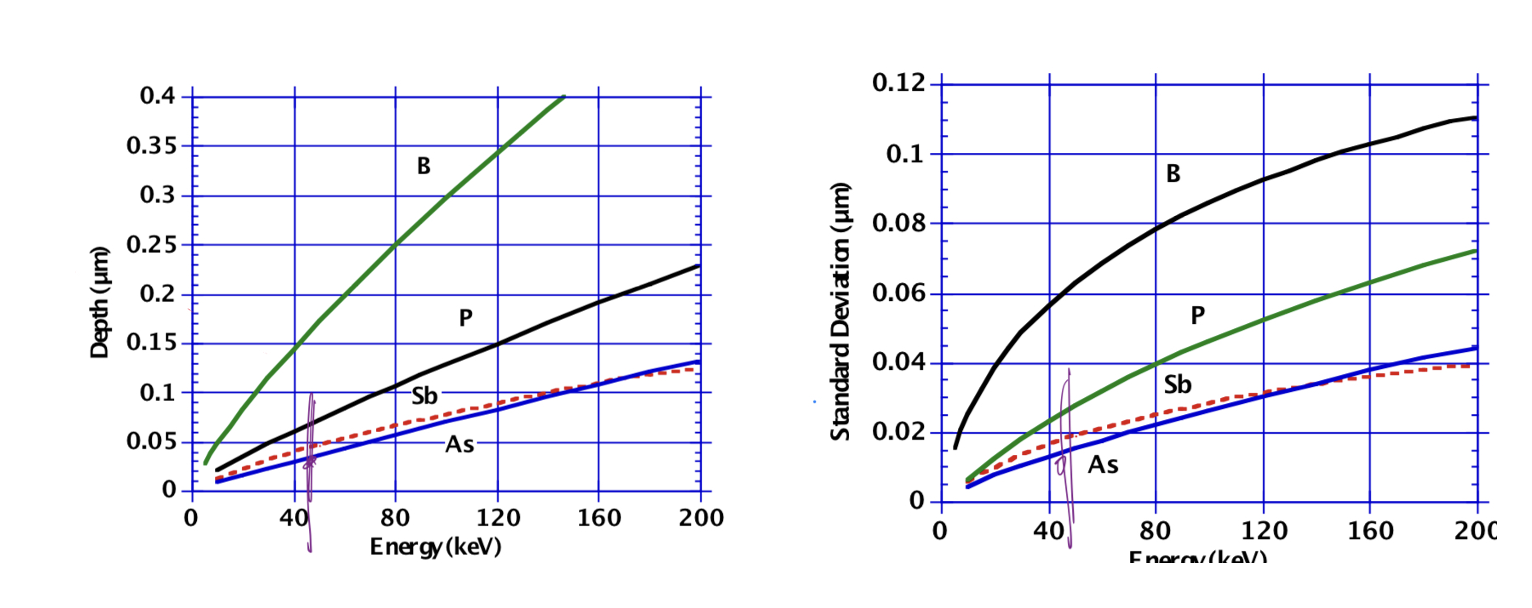
R_p와 △R_p를 구하면 되네요!
이는 문제에서 준 그래프에서 Arsenic의 경우 에너지 50 keV를 주었을 때 값을 읽으면 됩니다.
R_p = 35nm,
△R_p = 15nm,
Q = 2x10^15,
C(xm) = 10^16
이를 모두 대입해 주면 xm을 구할 수 있습니다.
xm = 0.105um
오늘은 여기까지입니다!
수식을 추가로 유도해 보는 것은 좋지만 외우려고 하진 않았으면 좋겠습니다!
수식을 공정상황에서 어떻게 이용할 수 있을지에 관해 아는 것이 중요하다고 생각해요
ion implantation은 여기서 마치겠습니다!
다음의 Lithography공정도 많이 기대해 주세요!
행복한 하루 보내세요 :)




댓글